Decoded: factor (coreutils)

[Back to Project Main Page]

Note: This page explores the design of command-line utilities. It is not a user guide.
[GNU Manual] [No POSIX requirement] [Linux man] [FreeBSD man]

Logical flow of factor command (coreutils)

Summary

factor - print prime factors

[Source] [Code Walkthrough]

Lines of code: 2662
Principal syscall: write() via printf()
Support syscalls: None
Options: 2 (help and version)

Descended from sort in Version 4 UNIX (1973)
Added to Textutils in December 1994 [First version]
Number of revisions: 152

The factor utility is a collection of distinct algorithms that try to solve the prime factor problem. The possible procedures are determined at compile time for that machine. We'll walk through the general utility design, leaving the math details to more authorative sources. The algorithms include:

Since I'm not a mathematician, I won't try to add insight to these implementations except to recommend reviewing Montgomery reductions and Hensel forms. The bottom line is speed -- especially far large input.

The utility also includes multiple implementations of the same algorithms: with and without the GNU Multiple Precision Arithmetic Library

Helpers:
  • do_stdin() - Tokenize stdin
  • factor() - Single-precision factor procedure
  • factor_insert_large() - Add a factor for single-precision input
  • factor_insert_multiplicity() - Add several factor multiples for single-precision input
  • factor_insert_refind() - Reproduce and add the discovered prime
  • factor_using_division() - Single-word trial division
  • factor_using_pollard_rho() - Single-word Pollard-Brent rho (up to 64-bits)
  • factor_using_pollard_rho2() - Double-word Pollard-Brent rho (up to 128-bits)
  • factor_using_squfof() - Square form factorization
  • gcd_odd() - Single-word GCD
  • gcd2_odd() - Double-word GCD
  • is_square() - Returns the root or 0 if not a square
  • isqrt() - Single-word square root
  • isqrt2() - Double-word square root
  • lbuf_alloc() - Initializes the line buffer
  • lbuf_flush() - Pushes the line buffer
  • lbuf_putc() - Adds a character to the line buffer
  • lbuf_putint() - Adds an integer to the line buffer
  • millerrabin() - Single-word Miller-Rabin algorithm
  • millerrabin2() - Double-word Miller-Rabin algorithm
  • mod2() - Double-word modulus
  • mp_factor() - Multi-precision factor procedure using GMP
  • mp_factor_clear() - Frees mp_factors
  • mp_factor_init() - Initializes mp_factors
  • mp_factor_insert() - Add a multi-precision factor
  • mp_factor_insert_ui() - Adds an unsigned integer to the mp_factors
  • mp_factor_using_division() - Multi-precision trial division using GMP
  • mp_factor_using_pollard_rho() - Multi-precision Pollard-Brent rho using GMP
  • mp_millerrabin() - Miller-Rabin using GMP
  • mp_prime_p() - Multi-precision primality testing using GMP
  • mpz_va_init() - Variadic multi-precision input parsing
  • mulredc() - Single-word Montgomery reduction
  • mulredc2() - Double-word Montgomery reduction
  • powm() - Single-word modular exponentiation
  • powm2() - Double-word modular exponentiation
  • prime_p() - Lucas primality test for single uint input
  • prime2_p() - Lucas primality test for double uint input
  • print_factors() - Starts factorization for all input
  • print_factors_single() - Starts factorization for a single input
  • print_uintmaxes() - Prints integers potentially stored as multiple ints
  • strto2uintmax() - Parses input numbers in to potentially multiple unsigned ints
Function-like macros:
  • add_ssaaaa() - Adds unsigned double-word values (no carry)
  • addmod() - Single-word modular addition
  • addmod2() - Double-word modular addition
  • count_leading_zeroes() - Counts the number of MSB zeroes
  • count_trailing_zeroes() - Counts the number of LSB zeroes
  • ge2() - Double-word greater-than or equal
  • gt2() - Double-word greater-than
  • lsh2() - Double-word left shift
  • rsh2() - Double-word right shift
  • sub_ddmmss() - Double-word subtraction
  • submod() - Single-word modular subtraction
  • submod2() - Double-word modular subtraction
  • udiv_qrnnd() - Divides unsigned double-word values
  • umul_ppmm() - Multiplies unsigned double-word values
External non-standard helpers:
  • die() - Exit with mandatory non-zero error and message to stderr
  • error() - Outputs error message to standard error with possible process termination

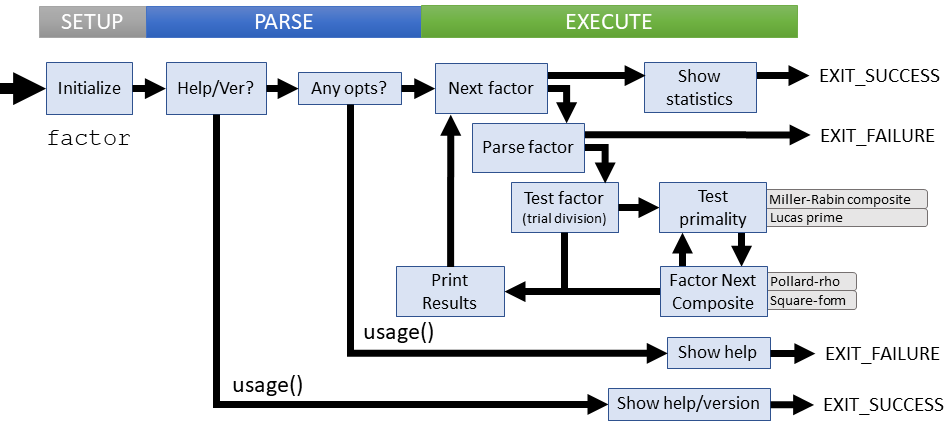
Setup

Two important data structure defined are struct factors and struct mp_factors. Both are used to store factor information with the former used for single precision (up to 128-bit) values and the latter for multi-precision. In general, all multi-precision operations are prefixed with mp_*.

After common initialization, main() allocates the line buffer (lbuf) which holds the output string.

Parsing

Parsing factor only checks the default help and version options. Any arguments are assumed to be numbers to be factored. The validity of factors is checked during execution.

Parsing may fail if the user provides an unknown option. The result is a short error message followed by the usage instructions.

Execution

The execution path for factor is more convoluted than a typical utility due to using the preprocessor for control flow. The definitions to watch for are:

  • HAVE_GMP - The GNU Multiple Precision Arithmetic Library is available to use
  • USE_SQUFOF - Defines (and prioritizes) square form factorization
  • STAT_SQUFOF - Output statistics. Not a branching decision (only extends computation)

The exact execution path is determined by both the machine capability and the size of the input. Multiple numbers may be input for testing. The general goal is to minimize execution time .

The basic flow for a single input number begins by determining if the input is single-precision (expressable 128-bits) or larger.

Factoring single-precision input

  • Check base cases (less than 2)
  • Try for a quick kill with trial division
    • Factor out powers of 2 (count number of LSB zeroes and shift)
    • Check the first 669 primes from the difference table
  • Check that any remaining value is significant (greater than 1)
  • Test the remaining value for prime (if so, we're done)
  • Factor the remaining composite with either square form (if available) or Pollard-Brent rho otherwise

Factoring values larger than 128 bits requires using GMP.

Failure cases:

  • Factoring a value larger than 128-bits without GMP
  • Attempting to factor a negative integer or non-integer
  • Primality test failure
  • Unable to write to output buffer

[Back to Project Main Page]